Time-Domain Reconstruction of Wide-Bandwidth Chirp
Richard T. Lord and Michael R. Inggs
Radar Remote Sensing Group, Dept of Electrical Engineering,
University of Cape Town
Private Bag, Rondebosch 7701, South Africa
Tel: +27 21 650 2799 Fax: +27 21 650
3465
Email: rlord-avoidspam@ebe.uct.ac.za
Note --- This document is a short summary of work that has already
been published [1, 2].
Some of the mathematical notation used in the published papers has changed
in this document, in order to clarify the analogy between this time-domain
method and the frequency-domain method
which reconstructs the target reflectivity function.
I. Introduction
This document describes a time-domain method to combine a group of n
narrow-bandwidth linear FM chirp pulses stepped in frequency in order to
construct a wide-bandwidth signal to achieve higher range resolution.
An advantage of this method is that it does not introduce any "ghost images''
in the high-resolution range profile.
II. Waveform Modelling
A linear FM chirp waveform at baseband can be described by
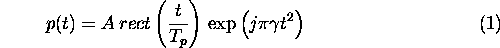
where A is the amplitude, 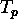 the pulse length and
the pulse length and 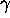 the chirp rate. The spectrum is approximately rectangular with bandwidth
the chirp rate. The spectrum is approximately rectangular with bandwidth 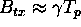 .
.
The transmitted RF signal is
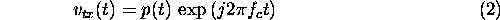
where 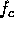 is the centre frequency. For a stepped-frequency system the carrier
frequency of pulse i, where i = 0, ..., (n - 1), is
given by
is the centre frequency. For a stepped-frequency system the carrier
frequency of pulse i, where i = 0, ..., (n - 1), is
given by

where 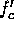 is the centre frequency of the reconstructed wide-bandwidth chirp pulse,
and
is the centre frequency of the reconstructed wide-bandwidth chirp pulse,
and 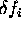 is the frequency shift associated with pulse i, given by
is the frequency shift associated with pulse i, given by
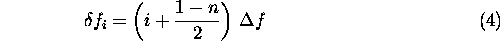
The transmitted pulses belonging to one burst can thus be described
by
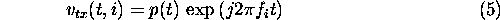
The received signal from a single scatterer at a distance 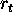 is given by
is given by
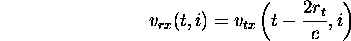
After coherent demodulation, the signal at baseband is given by
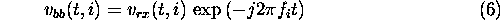
This signal is then sampled at a complex sampling rate of 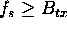 .
.
III. Reconstruction of Wide-Bandwidth Chirp
It is now proposed to reconstruct a wide-bandwidth chirp pulse in the time-domain
by coherently adding together several narrow-bandwith chirp pulses, each
obtained by separate transmission and reception of pulses of bandwidth 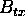 , but stepped appropriately in frequency by appropriate choice of the carrier
frequency. If the frequency step
, but stepped appropriately in frequency by appropriate choice of the carrier
frequency. If the frequency step 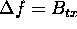 , the desired reconstruction is possible, otherwise there will be gaps
or overlaps in the corresponding wide-bandwidth spectrum. Figure
1 demonstrates the reconstruction process, showing
two narrow-bandwidth chirp pulses which are combined to form one wide-bandwidth
chirp pulse. The required signal processing steps are described below.
, the desired reconstruction is possible, otherwise there will be gaps
or overlaps in the corresponding wide-bandwidth spectrum. Figure
1 demonstrates the reconstruction process, showing
two narrow-bandwidth chirp pulses which are combined to form one wide-bandwidth
chirp pulse. The required signal processing steps are described below.
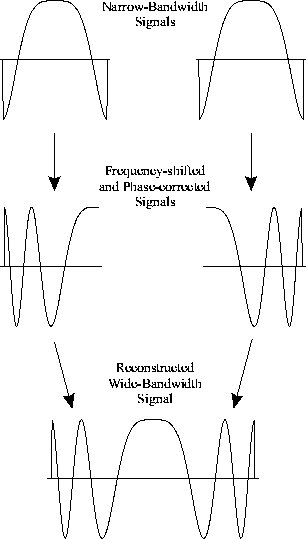 Figure 1: Reconstruction of wide-bandwidth chirp for n
= 2 transmitted pulses.
Figure 1: Reconstruction of wide-bandwidth chirp for n
= 2 transmitted pulses.
Upsampling
Unless the narrow-bandwidth pulses are already oversampled at a rate 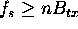 , they have to be upsampled before applying the frequency-shift described
below. Usually the time-domain signals have to be upsampled by a
factor of n, where n is the number of pulses used to synthesise
the wide bandwidth. The upsampling operation can be achieved by applying
an FFT, zero-padding the spectrum and then applying an IFFT.
, they have to be upsampled before applying the frequency-shift described
below. Usually the time-domain signals have to be upsampled by a
factor of n, where n is the number of pulses used to synthesise
the wide bandwidth. The upsampling operation can be achieved by applying
an FFT, zero-padding the spectrum and then applying an IFFT.
Frequency shift
The amount of frequency-shift associated with pulse i is given by 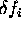 , which can be achieved in the time-domain by muliplication with the factor
, which can be achieved in the time-domain by muliplication with the factor 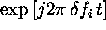 . The frequency-shifted pulses are thus described by
. The frequency-shifted pulses are thus described by
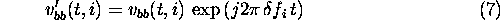
Phase correction
The need to add a phase-correcting term to each pulse can be explained
with the aid of Figure 2. In the figure, the phase
versus time plot of the wide-bandwidth signal and of the second narrow-bandwidth
signal (from a burst of 4) is shown. The narrow-bandwidth signal
has already been shifted in frequency and time, but a phase correcting
term given by
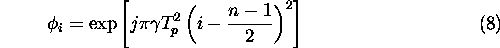
has to be added in order to avoid phase discontinuities in the wide-bandwith
signal.
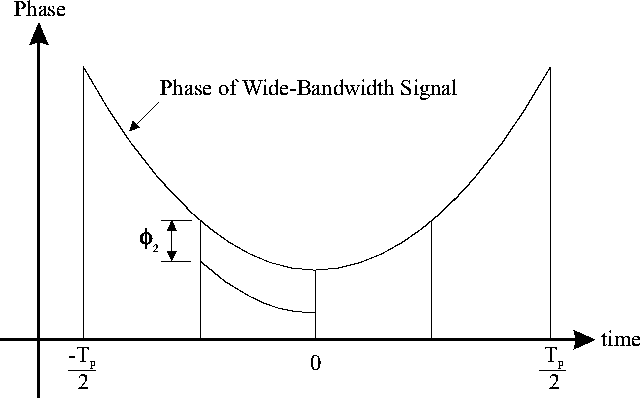 Figure 2: Addition of phase-correcting term to narrow-bandwidth
signals.
Figure 2: Addition of phase-correcting term to narrow-bandwidth
signals.
This phase term may be added to the narrow-bandwidth signals before
they are upsampled, thus requiring fewer multiplications and leading to
a faster implementation of the procedure.
Time shift
Before adding the narrow-bandwidth pulses together, they have to be shifted
in the time domain. The necessary time-shift is given by
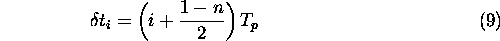
Since the signals are sampled at the A/D rate 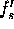 (after they have been upsampled), the time-shift given in terms of number
of samples is
(after they have been upsampled), the time-shift given in terms of number
of samples is

It is important that 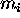 is an integer, because fractional values would have to be rounded, leading
to errors in the reconstructed wide-bandwidth signal. This requirement
can be achieved by adjusting either the pulse length
is an integer, because fractional values would have to be rounded, leading
to errors in the reconstructed wide-bandwidth signal. This requirement
can be achieved by adjusting either the pulse length 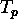 or the A/D sampling rate
or the A/D sampling rate 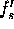 .
.
Combining narrow-bandwidth chirps
The reconstructed wide-bandwidth signal v'(t) is obtained
by coherently adding the processed narrow-bandwidth signals. Observing
that 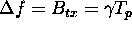 one obtains the following expression for v'(t) after simplification:
one obtains the following expression for v'(t) after simplification:
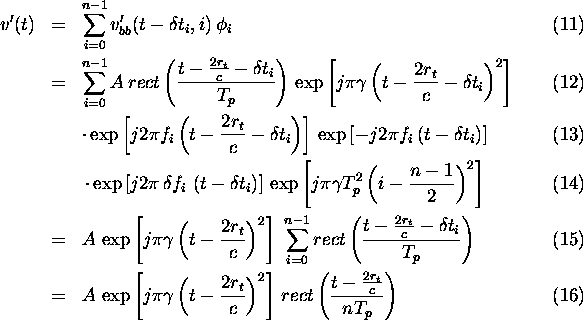
This is simply the expression of a wide-bandwidth chirp pulse with a
bandwidth of 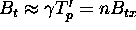 , with
, with 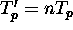 . Range compression may be achieved by convolving this signal with
a matched filter, which is given by the conjugate of the wide-bandwidth
pulse.
. Range compression may be achieved by convolving this signal with
a matched filter, which is given by the conjugate of the wide-bandwidth
pulse.
References
-
R.T. Lord and M.R. Inggs, "High Resolution SAR Processing
Using Stepped-Frequencies,'' Proc. IEEE Geoscience Remote Sensing Symp.,
IGARSS'97, Singapore, vol. 1, pp. 490-492, August 1997. igarss97.pdf
-
R.T. Lord and M.R. Inggs, "High Range Resolution Radar
using Narrowband Linear Chirps offset in Frequency,'' Proc. IEEE South
African Symp. on Communications and Signal Processing, COMSIG'97, Grahamstown,
South Africa, pp. 9-12, September 1997. comsig97.pdf
-
J.A. Scheer and J.L. Kurtz, Coherent Radar Performance Estimation, Norwood,
MA 02062: Artech House, 1993.
-
D.R. Wehner, High-Resolution Radar, Second Edition, Norwood, MA 02062:
Artech House, 1995.
Return to Richard Lord's Homepage.

![]()
![]() the pulse length and
the pulse length and ![]() the chirp rate. The spectrum is approximately rectangular with bandwidth
the chirp rate. The spectrum is approximately rectangular with bandwidth ![]() .
.
![]()
![]() is the centre frequency. For a stepped-frequency system the carrier
frequency of pulse i, where i = 0, ..., (n - 1), is
given by
is the centre frequency. For a stepped-frequency system the carrier
frequency of pulse i, where i = 0, ..., (n - 1), is
given by
![]()
![]() is the centre frequency of the reconstructed wide-bandwidth chirp pulse,
and
is the centre frequency of the reconstructed wide-bandwidth chirp pulse,
and ![]() is the frequency shift associated with pulse i, given by
is the frequency shift associated with pulse i, given by
![]()
![]()
![]() is given by
is given by
![]()
![]()
![]() .
.

![]()
![]()

![]()
![]() (after they have been upsampled), the time-shift given in terms of number
of samples is
(after they have been upsampled), the time-shift given in terms of number
of samples is
![]()
![]() is an integer, because fractional values would have to be rounded, leading
to errors in the reconstructed wide-bandwidth signal. This requirement
can be achieved by adjusting either the pulse length
is an integer, because fractional values would have to be rounded, leading
to errors in the reconstructed wide-bandwidth signal. This requirement
can be achieved by adjusting either the pulse length ![]() or the A/D sampling rate
or the A/D sampling rate ![]() .
.
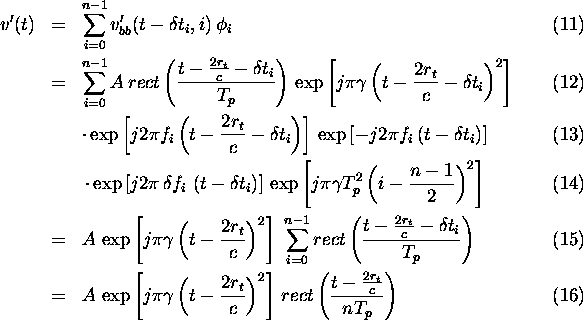
![]() , with
, with ![]() . Range compression may be achieved by convolving this signal with
a matched filter, which is given by the conjugate of the wide-bandwidth
pulse.
. Range compression may be achieved by convolving this signal with
a matched filter, which is given by the conjugate of the wide-bandwidth
pulse.