Stepped-Frequency Processing by Reconstruction of Target Reflectivity Spectrum
Andrew J. Wilkinson, Richard T. Lord and Michael R. Inggs
The authors are with the Radar Remote Sensing Group,
University of Cape Town, Rondebosch 7701, South Africa.
Phone +27 21 650 2799, Fax +27 21 650 3465, Email:
rlord-avoidspam@ebe.uct.ac.za.
Note --- This paper has been published at the Comsig'98 conference.
A pdf version of this paper can be downloaded here: comsig98b.pdf
Abstract --- This paper describes a processing technique for
combining stepped-frequency waveforms efficiently to obtain higher range
resolution. Essentially this method involves the reconstruction of a wider
portion of the target's reflectivity spectrum by combining the individual
spectra of the transmitted narrow-bandwidth pulses in the frequency domain.
This paper describes the signal processing steps involved, and shows simulation
results which validate and illustrate the method.
Keywords --- Stepped-frequency processing, synthetic range profile,
SRP, target reflectivity spectrum.
I. Introduction
The use of stepped-frequency waveforms to obtain high range resolution
is well documented [8, 10].
An advantage of the stepped-frequency approach for obtaining high range
resolution is the reduction of the instantaneous bandwidth and sampling
rate requirements of the radar system.
Synthetic range profile (SRP) processing is a very effective method
to obtain high-resolution downrange profiles of targets [10].
This method, however, has the unfortunate drawback that target energy spills
over into consecutive coarse range bins due to the matched filter operation,
causing ``ghost images'' in the resulting range profile [3].
This is the main reason why it is not regarded as a suitable method for
processing SAR images. A time-domain method which does not have this drawback
has already been demonstrated [5, 6].
However this method has been found to be inefficient due to the upsampling
requirement of the narrow-bandwidth signals.
Instead of recombining the stepped-frequency waveforms in the time-domain,
they can also be recombined in the frequency domain. Essentially the aim
is to reconstruct a larger portion of the target's reflectivity spectrum
by combining the individual spectra of the transmitted narrow-bandwidth
pulses in the frequency domain. The target reflectivity function 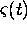 represents the target's reflection properties at range r mapped
into the time domain, where
represents the target's reflection properties at range r mapped
into the time domain, where 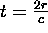 . The principle of enhancing the range resolution by recovering a larger
band of the reflectivity's spectrum was introduced by Prati and Rocca [7],
but in the context of coherent combination of SAR images taken from different
observation angles. In this paper we show how this concept may be applied
to the concept of stepped-frequency processing, and describe the signal
processing steps involved.
. The principle of enhancing the range resolution by recovering a larger
band of the reflectivity's spectrum was introduced by Prati and Rocca [7],
but in the context of coherent combination of SAR images taken from different
observation angles. In this paper we show how this concept may be applied
to the concept of stepped-frequency processing, and describe the signal
processing steps involved.
II. Waveform Modelling
A linear FM chirp waveform at baseband can be described by
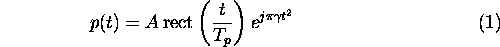
where A is the amplitude, 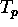 the pulse length and
the pulse length and 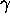 the chirp rate. The spectrum is approximately rectangular with bandwidth
the chirp rate. The spectrum is approximately rectangular with bandwidth 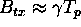 . This is a good approximation for linear FM chirp pulses with a high time-bandwidth
product.
. This is a good approximation for linear FM chirp pulses with a high time-bandwidth
product.
The transmitted RF signal is modelled by
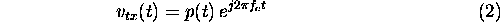
where 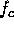 is the centre frequency. The received signal is given by the convolution
of the scene reflectivity function
is the centre frequency. The received signal is given by the convolution
of the scene reflectivity function 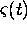 and the transmitted pulse:
and the transmitted pulse:
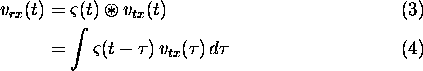
After coherent demodulation, the signal at baseband is given by
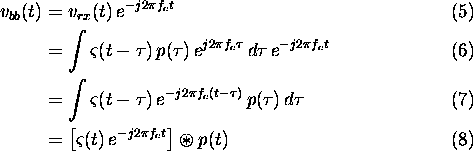
In accordance with the Nyquist criteria, the I and Q
channels of this complex signal are each sampled at a sampling rate of 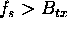 . Fourier transforming
. Fourier transforming 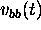 we obtain
we obtain
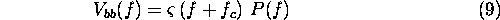
Thus, the spectral representation of the received signal can be viewed
as a windowed version of the target's reflectivity spectrum 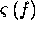 , where the position of the window is determined by the centre frequency,
and the shape is determined by the spectrum of the transmitted pulse.
, where the position of the window is determined by the centre frequency,
and the shape is determined by the spectrum of the transmitted pulse.
Range compression is achieved by convolving the received signal with
a linear compression filter H(f), designed as a trade-off
between compressing the received signal into a narrow pulse (with desirable
low sidelobe properties) and improving the signal to noise ratio. In the
frequency domain the range-compression operation is given by
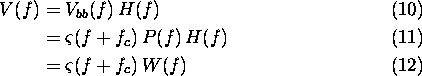
where 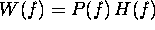 . The time-domain signal is
. The time-domain signal is

The phase of H(f) is always chosen to cancel the phase
of P(f), thus 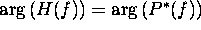 . The amplitude of H(f) is chosen according to the desired
time-domain impulse response. For example, if we assume that P(f)
is strictly bandlimited to
. The amplitude of H(f) is chosen according to the desired
time-domain impulse response. For example, if we assume that P(f)
is strictly bandlimited to  , and if
, and if  across that bandwidth, then
across that bandwidth, then

This is simply a bandlimited, shifted version of the target's reflectivity
spectrum. Inverse transforming, the time-domain waveform is
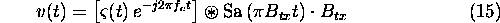
where 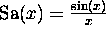 . Thus the time-domain impulse response is a sinc function with
a
. Thus the time-domain impulse response is a sinc function with
a 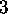 dB resolution of
dB resolution of 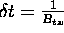 . The sidelobe response can be reduced by introducing an appropriate frequency-domain
window function, at the expense of widening the mainlobe.
. The sidelobe response can be reduced by introducing an appropriate frequency-domain
window function, at the expense of widening the mainlobe.
III. Reconstruction of Target Spectrum
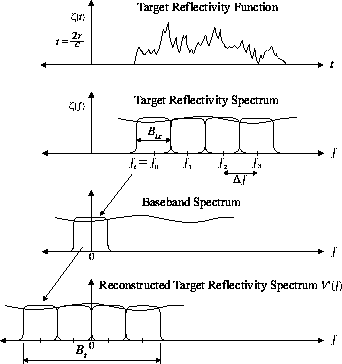 Figure 1: Reconstruction of the target reflectivity spectrum
for n=4 transmitted pulses,
each with carrier frequency
Figure 1: Reconstruction of the target reflectivity spectrum
for n=4 transmitted pulses,
each with carrier frequency 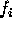 and bandwidth
and bandwidth 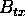
It is now proposed to reconstruct a wider portion of the target's reflectivity
spectrum by piecing together several adjacent subportions of the spectrum,
each obtained by separate transmission and reception of pulses of bandwidth 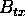 , but stepped appropriately in frequency by appropriate choice of the carrier
frequency. If the frequency step
, but stepped appropriately in frequency by appropriate choice of the carrier
frequency. If the frequency step 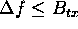 , the desired reconstruction is possible. Assuming a sequence of n
adjacent windows (indexed by
, the desired reconstruction is possible. Assuming a sequence of n
adjacent windows (indexed by 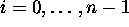 ),
a broad region of the frequency spectrum can be reconstructed, symmetrical
about zero, by shifting each spectrum at baseband by an amount
),
a broad region of the frequency spectrum can be reconstructed, symmetrical
about zero, by shifting each spectrum at baseband by an amount
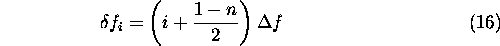
in the positive direction, and adding together the shifted versions.
If we assume a linear superposition of the shifted subspectra, the
reconstructed spectrum as shown in Figure 1
is
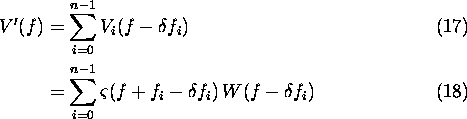
where 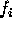 is the carrier frequency of pulse i and
is the carrier frequency of pulse i and 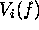 is the frequency spectrum at baseband of pulse i. The shift
is the frequency spectrum at baseband of pulse i. The shift 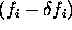 can, by substitution and simplification, be seen to be the centre frequency
can, by substitution and simplification, be seen to be the centre frequency 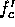 of the entire reconstructed spectrum:
of the entire reconstructed spectrum:
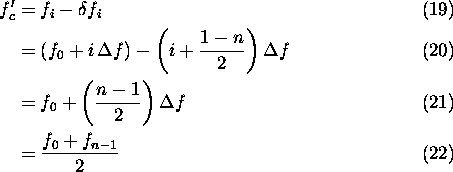
The reconstructed spectrum can thus be expressed as
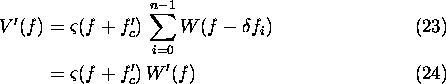
where
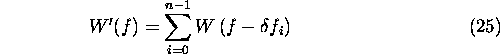
The time-domain signal can then be obtained by inverse transforming
to yield
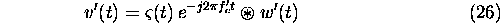
If, for example, we consider the case where the frequency step 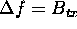 , then the total bandwidth of the reconstructed spectrum is
, then the total bandwidth of the reconstructed spectrum is 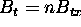 , as is shown in Figure 1. If the combined compression
filter
, as is shown in Figure 1. If the combined compression
filter
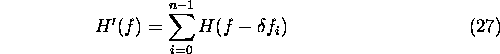
is chosen such that 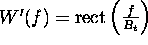 , then the time-domain signal is
, then the time-domain signal is
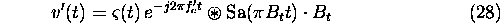
and the 3dB resolution is 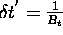 , which is a factor of n better than would have been achieved without
reconstruction.
, which is a factor of n better than would have been achieved without
reconstruction.
IV. Practical Implementation on Sampled Data
The steps below describe how the spectral reconstruction can be performed
with sampled data.
-
Choose a range of carrier frequencies
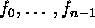 spaced at
spaced at 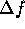 equal to, or marginally less than
equal to, or marginally less than 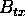 . If
. If 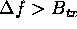 , the reconstructed spectrum will contain gaps and the resulting time-domain
range profile will possess undesirable properties in the form of repeated
artifacts spaced at multiples of
, the reconstructed spectrum will contain gaps and the resulting time-domain
range profile will possess undesirable properties in the form of repeated
artifacts spaced at multiples of 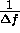 . However even if there are gaps, an improvement in mainlobe resolution
is still possible.
. However even if there are gaps, an improvement in mainlobe resolution
is still possible.
-
For each pulse obtain a sampled version of
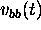 , starting at
, starting at 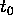 , with
, with 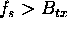 being the complex sample rate.
being the complex sample rate.
-
Apply an FFT to each sampled pulse to obtain the individual subspectra
of the target's reflectivity spectrum.
-
To obtain an optimal SNR, it is important to sum the signals with
appropriate weighting in the overlap regions. This may be realised by matched-filtering
each subspectra prior to addition.
-
Since
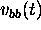 was sampled starting at
was sampled starting at 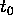 , each subspectrum has to be multiplied by the delay compensation factor
, each subspectrum has to be multiplied by the delay compensation factor 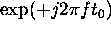 .
.
-
Shift the spectrum of pulse i to its appropriate location,
centred on
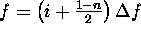 .
.
-
Form the combined spectrum by coherently adding the individual subspectra
(see Figure 2).
-
Multiply the combined spectrum by the compression filter
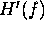 (see Figure 3) to obtain the discrete equivalent
of
(see Figure 3) to obtain the discrete equivalent
of 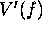 (see Figure 4).
(see Figure 4).
-
Multiply the entire spectrum with
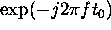 . This re-shifts the time domain back to a sampled set beginning at
. This re-shifts the time domain back to a sampled set beginning at 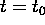 .
.
-
Apply a reshaping window to tailor the time domain response (see
Figure 4). This could be a standard Hanning or
Taylor window.
-
Inverse FFT the entire spectrum to obtain the high-resolution range
profile (see Figure 5).
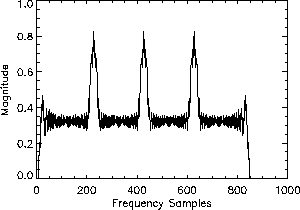 Figure 2: Spectrum obtained after coherent addition of frequency-shifted
subspectra.
Figure 2: Spectrum obtained after coherent addition of frequency-shifted
subspectra.
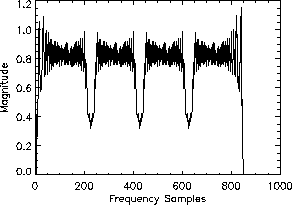 Figure 3: Spectrum of compression filter
Figure 3: Spectrum of compression filter 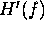 .
.
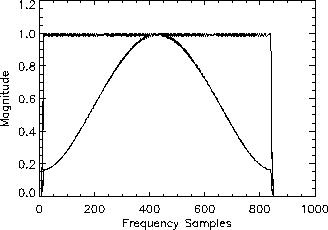 Figure 4: Target reflectivity spectrum
Figure 4: Target reflectivity spectrum 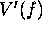 after applying compression filter,
and after applying reshaping window.
after applying compression filter,
and after applying reshaping window.
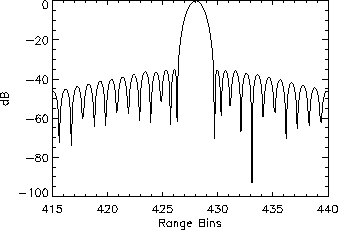 Figure 5: Section of high-resolution range profile showing
point target.
Figure 5: Section of high-resolution range profile showing
point target.
V. Design of Compression Filter
The design of the compression filter 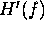 is the most critical and important step in this method. It is important
to consider the following points when constructing this filter:
is the most critical and important step in this method. It is important
to consider the following points when constructing this filter:
-
Obtain an estimate of the impulse response spectrum
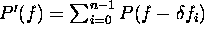 . Ideally, for a real system, this should be achieved by measuring the
return of a real, physical point target, for example a corner reflector,
and recombining the individual spectra as described in the previous section.
For such a target
. Ideally, for a real system, this should be achieved by measuring the
return of a real, physical point target, for example a corner reflector,
and recombining the individual spectra as described in the previous section.
For such a target 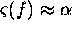 , where
, where 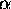 is a constant, and therefore the combined baseband spectrum would be
is a constant, and therefore the combined baseband spectrum would be 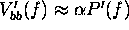 . This method automatically includes receiver distortions.
. This method automatically includes receiver distortions.
-
If it is impractical or impossible to obtain the return of a real,
physical point target, a point target simulation may be used. It might
be difficult, however, to predict receiver distortions. Note that the position
of the high-resolution profile will be relative to the target range chosen
in the simulation and may therefore need to be shifted.
-
If the sampled data has already been range-compressed by a matched
filter to optimise SNR, the subspectra used in constructing
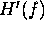 must also be range-compressed first.
must also be range-compressed first.
-
When using a simulation it is important to ensure that there is no
aliasing and that the individual subspectra are bandlimited.
-
Having obtained an approximation of
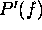 , the filter
, the filter 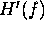 is piecewise defined as follows:
is piecewise defined as follows:
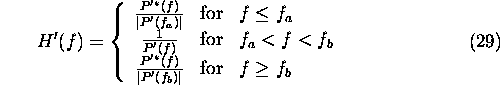
where the region 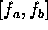 includes the major part of the reconstructed spectrum, containing all the
subspectra boundaries. This will effectively smoothen any ripples at the
subspectra boundaries, yielding the desired time-domain impulse response.
The first section and the last section of
includes the major part of the reconstructed spectrum, containing all the
subspectra boundaries. This will effectively smoothen any ripples at the
subspectra boundaries, yielding the desired time-domain impulse response.
The first section and the last section of 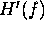 , where the target spectrum decays to zero, is equated to the conjugate
of
, where the target spectrum decays to zero, is equated to the conjugate
of 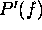 . This prevents the amplification of noise for a real system, while still
cancelling the phase correctly. Note that
. This prevents the amplification of noise for a real system, while still
cancelling the phase correctly. Note that 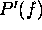 has to be scaled appropriately so that no discontinuities arise at
has to be scaled appropriately so that no discontinuities arise at 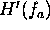 and
and 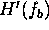 .
.
VI. Simulation Results
A stepped-frequency radar system was simulated to validate and illustrate
the method described above. Table I summarises the relevant parameters
used. Four transmitter pulses were simulated, each with a bandwidth of
30 MHz, spaced at 25MHz intervals, with an overlap of 5 MHz between adjacent
subspectra. The total radar bandwidth is 105MHz.
Table I: Simulation Parameters
| first centre frequency |
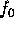 |
5.2625 GHz |
| frequency step size |
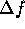 |
25 MHz |
| number of steps |
n |
4 |
| total radar bandwidth |
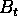 |
105 MHz |
| pulse length |
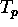 |
5 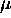 s
s |
| chirp bandwidth |
B |
30 MHz |
| ADC (complex) sample rate |
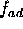 |
32 MHz |
Figure 2 shows the magnitude of the reconstructed
target reflectivity spectrum. The ``ripples'' at the three subspectra boundaries
are clearly visible. After applying the compression filter shown in Figure
3 one obtains the spectrum shown in Figure 4,
which closely approximates the desired 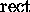 function. A window function has been applied to this spectrum to reduce
sidelobe levels. Inverse Fourier transforming this spectrum yields the
time-domain high-resolution profile. A dB-plot of a section of this profile
is shown in Figure 5, with sidelobe levels at approximately
-35dB.
function. A window function has been applied to this spectrum to reduce
sidelobe levels. Inverse Fourier transforming this spectrum yields the
time-domain high-resolution profile. A dB-plot of a section of this profile
is shown in Figure 5, with sidelobe levels at approximately
-35dB.
VII. Conclusions
The method described in this paper efficiently uses all the information
obtained from the stepped-frequency waveforms to produce a high-resolution
range profile of the illuminated target scene. The execution of the signal
processing steps is fast compared to time-domain implementations, since
only FFTs and phase multiplications are required, and no upsampling of
the narrow-bandwidth pulses is necessary. Furthermore this method is extremely
flexible in the sense that the individual pulses may have different bandwidths,
the frequency spacing between pulses may vary, the subspectra may (should)
overlap in the frequency domain and the individual frequency steps may
already be range-compressed. The resulting range profile does not suffer
from multiple ``ghost'' images, except if the construction of the compression
filter 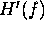 is such that the reconstructed target spectrum contains ripples at the
subspectra boundaries. It is therefore important that great care is invested
in the design of the compression filter.
is such that the reconstructed target spectrum contains ripples at the
subspectra boundaries. It is therefore important that great care is invested
in the design of the compression filter.
Acknowledgments
The authors wish to thank Rolf Lengenfelder, whose radar simulator was
used to create the simulated data, and Jasper Horrell for his suggestions
and advice.
References
-
1
-
A. Gustavsson, P.O. Frölind, H. Hellsten, T. Jonsson, B. Larsson
and G. Stenström, ``The Airborne VHF SAR System CARABAS,'' Proc.
IEEE Geoscience Remote Sensing Symp., IGARSS'93, Tokyo, Japan, vol.
2, pp. 558-562, August 1993.
-
2
-
Y. Huang, Z. Ma and S. Mao, ``Stepped-frequency SAR System Design
and Signal Processing,'' Proc. European Conference on Synthetic Aperture
Radar, EUSAR'96, Königswinter, Germany, pp. 565-568, March 1996.
-
3
-
M.R. Inggs, M.W. van Zyl and A. Knight, ``A Simulation of Synthetic
Range Profile Radar,'' Proc. IEEE South African Symp. on Communications
and Signal Processing, COMSIG'92, Cape Town, South Africa, pp. 1-6,
September 1992.
-
4
-
R.T. Lord and M.R. Inggs, ``High Resolution VHF SAR Processing Using
Synthetic Range Profiling,'' Proc. IEEE Geoscience Remote Sensing Symp.,
IGARSS'96, Lincoln, Nebraska, vol. 1, pp. 454-456, June 1996. igarss96.pdf
-
5
-
R.T. Lord and M.R. Inggs, ``High Resolution SAR Processing Using
Stepped-Frequencies,'' Proc. IEEE Geoscience Remote Sensing Symp.,
IGARSS'97, Singapore, vol. 1, pp. 490-492, August 1997. igarss97.pdf
-
6
-
R.T. Lord and M.R. Inggs, ``High Range Resolution Radar using Narrowband
Linear Chirps offset in Frequency,'' Proc. IEEE South African Symp.
on Communications and Signal Processing, COMSIG'97, Grahamstown, South
Africa, pp. 9-12, September 1997. comsig97.pdf
-
7
-
C. Prati and F. Rocca, ``Range Resolution Enhancement with Multiple
SAR Surveys Combination,'' IEEE, 1992.
-
8
-
J.A. Scheer and J.L. Kurtz, Coherent Radar Performance Estimation,
Norwood, MA 02062: Artech House, 1993.
-
9
-
L.M.H. Ulander and H. Hellsten, ``System Analysis of Ultra-Wideband
VHF SAR,'' RADAR'97, Edinburgh, UK, Included in conference publication
no. 449, pp. 104-108, IEE, London, October 1997.
-
10
-
D.R. Wehner, High-Resolution Radar, Second Edition, Norwood,
MA 02062: Artech House, 1995.
-
-
-
-
Return to Richard Lord's Homepage.
-
-
-

-
-
![]() represents the target's reflection properties at range r mapped
into the time domain, where
represents the target's reflection properties at range r mapped
into the time domain, where ![]() . The principle of enhancing the range resolution by recovering a larger
band of the reflectivity's spectrum was introduced by Prati and Rocca [7],
but in the context of coherent combination of SAR images taken from different
observation angles. In this paper we show how this concept may be applied
to the concept of stepped-frequency processing, and describe the signal
processing steps involved.
. The principle of enhancing the range resolution by recovering a larger
band of the reflectivity's spectrum was introduced by Prati and Rocca [7],
but in the context of coherent combination of SAR images taken from different
observation angles. In this paper we show how this concept may be applied
to the concept of stepped-frequency processing, and describe the signal
processing steps involved.
![]()
![]() the pulse length and
the pulse length and ![]() the chirp rate. The spectrum is approximately rectangular with bandwidth
the chirp rate. The spectrum is approximately rectangular with bandwidth ![]() . This is a good approximation for linear FM chirp pulses with a high time-bandwidth
product.
. This is a good approximation for linear FM chirp pulses with a high time-bandwidth
product.
![]()
![]() is the centre frequency. The received signal is given by the convolution
of the scene reflectivity function
is the centre frequency. The received signal is given by the convolution
of the scene reflectivity function ![]() and the transmitted pulse:
and the transmitted pulse:
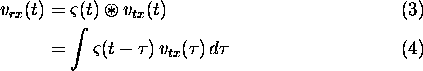
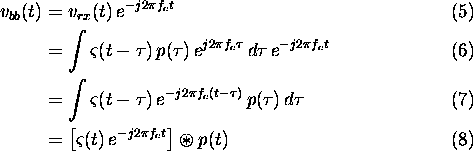
![]() . Fourier transforming
. Fourier transforming ![]() we obtain
we obtain
![]()
![]() , where the position of the window is determined by the centre frequency,
and the shape is determined by the spectrum of the transmitted pulse.
, where the position of the window is determined by the centre frequency,
and the shape is determined by the spectrum of the transmitted pulse.
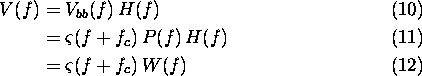
![]() . The time-domain signal is
. The time-domain signal is
![]()
![]() . The amplitude of H(f) is chosen according to the desired
time-domain impulse response. For example, if we assume that P(f)
is strictly bandlimited to
. The amplitude of H(f) is chosen according to the desired
time-domain impulse response. For example, if we assume that P(f)
is strictly bandlimited to ![]() , and if
, and if ![]() across that bandwidth, then
across that bandwidth, then
![]()
![]()
![]() . Thus the time-domain impulse response is a sinc function with
a
. Thus the time-domain impulse response is a sinc function with
a ![]() dB resolution of
dB resolution of ![]() . The sidelobe response can be reduced by introducing an appropriate frequency-domain
window function, at the expense of widening the mainlobe.
. The sidelobe response can be reduced by introducing an appropriate frequency-domain
window function, at the expense of widening the mainlobe.

![]()
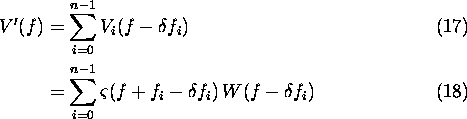
![]() is the carrier frequency of pulse i and
is the carrier frequency of pulse i and ![]() is the frequency spectrum at baseband of pulse i. The shift
is the frequency spectrum at baseband of pulse i. The shift ![]() can, by substitution and simplification, be seen to be the centre frequency
can, by substitution and simplification, be seen to be the centre frequency ![]() of the entire reconstructed spectrum:
of the entire reconstructed spectrum:
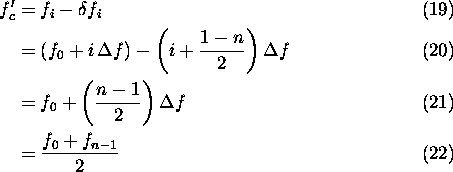
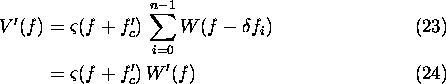
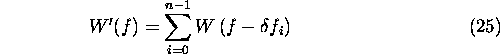
![]()
![]() , then the total bandwidth of the reconstructed spectrum is
, then the total bandwidth of the reconstructed spectrum is ![]() , as is shown in Figure 1. If the combined compression
filter
, as is shown in Figure 1. If the combined compression
filter
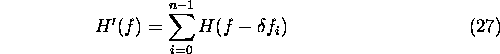
![]() , then the time-domain signal is
, then the time-domain signal is
![]()
![]() , which is a factor of n better than would have been achieved without
reconstruction.
, which is a factor of n better than would have been achieved without
reconstruction.




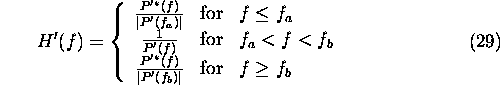
![]() includes the major part of the reconstructed spectrum, containing all the
subspectra boundaries. This will effectively smoothen any ripples at the
subspectra boundaries, yielding the desired time-domain impulse response.
The first section and the last section of
includes the major part of the reconstructed spectrum, containing all the
subspectra boundaries. This will effectively smoothen any ripples at the
subspectra boundaries, yielding the desired time-domain impulse response.
The first section and the last section of ![]() , where the target spectrum decays to zero, is equated to the conjugate
of
, where the target spectrum decays to zero, is equated to the conjugate
of ![]() . This prevents the amplification of noise for a real system, while still
cancelling the phase correctly. Note that
. This prevents the amplification of noise for a real system, while still
cancelling the phase correctly. Note that ![]() has to be scaled appropriately so that no discontinuities arise at
has to be scaled appropriately so that no discontinuities arise at ![]() and
and ![]() .
.![]() function. A window function has been applied to this spectrum to reduce
sidelobe levels. Inverse Fourier transforming this spectrum yields the
time-domain high-resolution profile. A dB-plot of a section of this profile
is shown in Figure 5, with sidelobe levels at approximately
-35dB.
function. A window function has been applied to this spectrum to reduce
sidelobe levels. Inverse Fourier transforming this spectrum yields the
time-domain high-resolution profile. A dB-plot of a section of this profile
is shown in Figure 5, with sidelobe levels at approximately
-35dB.