Approaches to RF Interference Suppression for VHF/UHF Synthetic Aperture
Radar
Richard T. Lord and Michael R. Inggs
The authors are with the Radar Remote Sensing Group,
University of Cape Town, Rondebosch 7701, South Africa.
Phone +27 21 650 2799, Fax +27 21 650 3465, Email:
rlord-avoidspam@ebe.uct.ac.za.
Note --- This paper has been published at
the Comsig'98 conference. A pdf version of this paper can be downloaded
here:
comsig98a.pdf
Abstract --- An increasing amount of interest
has developed in VHF/UHF SAR applications. Unfortunately the VHF-UHF portion
of the spectrum is already in heavy use by other services, such as television
and mobile communications. Even in remote locations the interference power
often exceeds receiver noise by many dB, becoming the limiting factor on
system sensitivity and severely degrading the image quality. This paper
addresses the problem of radio frequency (RF) interference and its impact
on SAR imagery. Several RF interference suppression methods are described
and discussed. These include spectral estimation and coherent subtraction
algorithms, as well as various filter approaches. The least-mean-squared
(LMS) adaptive filter is described in detail, and its effectiveness in
suppressing RF interference is demonstrated on simulated data and on real
P-Band data.
Keywords --- Radio frequency interference, RFI, LMS adaptive
filter, synthetic aperture radar, SAR, VHF, UHF.
1 Introduction
Ultrawideband radar has proven to be a very powerful method for underground
and obscured object detection. The combination of using low frequencies
(which exhibit very good foliage and ground penetrating capabilities) such
as VHF/UHF or even lower, and using wideband pulses (which provide high
range resolution), creates a wide variety of applications, making these
radar systems extremely useful. Such applications include the detection
of targets concealed by foliage and/or camouflage, detection of buried
objects, detection and location of buried pipes and cables, and archaeological
and geological exploration, such as the location of underground riverbeds.
However these frequency bands are already in use by other services such
as television, mobile communications, radio and cellular phones. The interference
power received from these emitters often exceeds the receiver noise by
many dB, thereby limiting the system sensitivity. Regulatory sanctions
do not allow the increase of radar power, so that prior services are not
appreciably degraded. Therefore it is important to investigate possible
means of suppressing the interference in the received signal.
Suppressing radio interference from a received signal essentially involves
three steps [1]:
-
Finding a model to parameterise the interfering signals,
-
estimating the parameters of the interfering signals using the measured
data, and
-
using the estimated parameters to suppress the interference in the
data.
Section 2 discusses the model which is commonly used
to parameterise the interfering signals, and Section 3
gives a very brief literature review of approaches that have been used
successfully to suppress RF interference. An approach that has received
very favourable review is the least-mean-squared (LMS) adaptive filter
[1, 10, 16].
It is described in detail in Section 4, and the results
that have been obtained from simulated data and from real P-Band data are
discussed in Section 5 and Section 6
respectively.
2 Modelling the RFI Environment
It is important to describe the interference environment as accurately
as possible. This includes statistics on the density of the interference
emitters, identity (type) of emitters, effective radiated power, modulation
bandwidth, duty factor and temporal dependence. The most direct way to
achieve this is to make use of ``sniffer'' pulses or ``listening beforehand''
schemes, however this is not yet generally implemented in practice. Although
this method is useful for many signal processing methods, its effectiveness
depends strongly on how long the RFI remains coherent.
Most approaches model the RFI as a superposition of single sinusoidal
``tones'', and the wideband signal plus system noise as white noise. Surveys
performed by the Grumman E-2C UHF radar (420-450MHz) [9]
have shown that 50% of emitters have a spectral bandwidth between 0-50kHz
(single channel voice/radio telegraphy), 40% between 50-150kHz and less
than 10% have a bandwidth greater than 150kHz (data communications, multichannel
telephony, etc.)
It is important to estimate the modulation time of the RFI, which is
the inverse of the RFI bandwidth, in order to predict whether the parameters
of the modelled sinusoidal interference change across one range line, i.e.
whether the tone model of the RFI breaks down. According to Braunstein
et al [2], most RFI has a modulation
time of 5-10 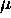 s, which is consistent with an effective bandwidth of a few hundred kHz
or less.
s, which is consistent with an effective bandwidth of a few hundred kHz
or less.
3 Approaches to RFI Suppression
RFI suppression algorithms fall into two classes, namely (1) spectral estimation
and coherent subtraction approaches and (2) various filter approaches.
The relative merits and disadvantages of these approaches are discussed
in the following subsections. One approach that has not been investigated
is the creation of antenna pattern nulls in the direction of the RFI source
as a means for suppressing the interference.
3.1 Spectral estimation and coherent subtraction approaches
These approaches have been shown to be extremely effective and powerful
to the extent that the model of RFI as a superposition of sinusoids is
true. They require the frequency, phase and amplitude 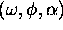 of each interfering sinusoid to be estimated, after which the sinusoids
are subtracted from the contaminated signal. The performance is excellent
in terms of low signal distortion and good interference suppression, however
the effectiveness is reduced for high modulation bandwidths, since the
parameters change over the record length. For computational efficiency
and effectiveness, these methods must be ``tuned'' to use a priori
knowledge, such as where the FM-broadcast band is located [13].
Furthermore the parameters of the tones (especially the phase) must be
estimated for every pulse.
of each interfering sinusoid to be estimated, after which the sinusoids
are subtracted from the contaminated signal. The performance is excellent
in terms of low signal distortion and good interference suppression, however
the effectiveness is reduced for high modulation bandwidths, since the
parameters change over the record length. For computational efficiency
and effectiveness, these methods must be ``tuned'' to use a priori
knowledge, such as where the FM-broadcast band is located [13].
Furthermore the parameters of the tones (especially the phase) must be
estimated for every pulse.
Braunstein et al [2] have achieved
very good results using a maximum likelihood estimate (MLE) approach.
For a single sinusoid in white noise the parameter vector 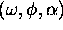 can be found analytically, however for multiple sinusoids it becomes an
extremely difficult nonlinear problem involving 3m variables, where
m is the number of sinusoids to be estimated. An efficient technique
to overcome this problem is to use an iterative algorithm, where the initial
guess of the estimates is iteratively improved. The initial guess may be
obtained from the data spectrum by applying an FFT. Another method would
be to model the RFI, signal and noise as an autoregressive (AR)
process [1, 12]. The estimate
can be found analytically, however for multiple sinusoids it becomes an
extremely difficult nonlinear problem involving 3m variables, where
m is the number of sinusoids to be estimated. An efficient technique
to overcome this problem is to use an iterative algorithm, where the initial
guess of the estimates is iteratively improved. The initial guess may be
obtained from the data spectrum by applying an FFT. Another method would
be to model the RFI, signal and noise as an autoregressive (AR)
process [1, 12]. The estimate 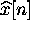 of the nth sample of the measured data is given by
of the nth sample of the measured data is given by
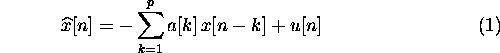
where p is the order of the model, indicating that p/2
sinusoids can be estimated, a[k] are the autoregressive parameters
which need to be derived from the measured data, and u[k]
is the signal plus noise (without interference). According to Braunstein
et al [2] the results obtained using
this method are similar to those obtained using the MLE method.
Golden et al [7] used a parametric
maximum likelihood (PML) algorithm for the estimation of the parameters
of the RFI tones. This algorithm is also applied to deramp SAR. It is claimed
that 90-95% of the RFI that could have corrupted a SAR image is removed.
The number of iterations through the PML algorithm at each threshold is
approximately equal to the number of tones being estimated.
Miller et al [13] have developed a chirp-least-squares
algorithm with clipping (CLSC). The following advantages are claimed,
compared to adaptive FIR filtering:
-
An estimate-and-subtract algorithm provides the narrowest possible stop-band
for a given data length and therefore minimises time-sidelobes.
-
The CLSC technique allows iterative, nonlinear signal (target) excision,
which reduces sidelobes and signal loss even further.
-
There are no filter edge effects.
This method makes use of a priori knowledge of the RFI environment.
A non-least-squares approach is used to model FM signals, which vary by
as much as 75kHz from the centre frequency.
Ferrell [5] has developed a method which requires
2-D compression of the SAR image (containing both signal and interference),
after which a second compressed SAR image (containing only interference)
is coherently subtracted. This requires two arrays of data to be collected
in an interleaved manner, which might require the PRF to be increased by
a factor of 2. It is claimed that this method leaves the target and clutter
phase history essentially intact.
3.2 Filter approaches
A common suppression approach is to examine the spectrum of the contaminated
signal, identify the interference spikes which are usually many dB larger
than the signal, and then to remove these spikes with a notch filter. Although
the notching concept is effective for very narrowband interferers and a
small number of emitters, it can also produces adverse effects on the overall
radar system performance [9], such as reducing
image intensity, reducing range resolution, creating loss in the target's
integrated signal to noise ratio and introducing time-sidelobes.
Koutsoudis and Lovas [9] describe an RFI
Minimisation algorithm developed by Grumman Aerospace Corporation,
which is based on least-mean-squared estimation theory. A single filter
is used to achieve both the interference suppression as well as the equalisation
needed to overcome the distortions caused by the notching function. This
method has been tested extensively using numerous data sets and excellent
performance results have been obtained for all scenarios.
Buckreuss [3] has implemented a notch filter
to suppress RF interference in contaminated P-Band data. The interferences
have been removed to a large extent, with some sidelobes visible in areas
with intense backscatter, as well as a slight degradation of the contrast.
Abend and McCorkle [1] have achieved good results
using an adaptive FIR filter approach. The adaptive filter is an over-determined
system producing a FIR filter with n taps, independent of the number
of interfering signals. As opposed to tone extraction methods, this method
simultaneously eliminates hundreds of narrowband interferers. A low update
rate for the filter tap weights is allowed, since the filter weights were
found to be effective for hundreds of subsequent radar pulses. Furthermore,
minimal computational complexity is required, making this a very fast method.
An iterative technique has been used to reduce the range sidelobes caused
by the filter's impulse response. The adaptive filter is based on an autoregressive
(AR) all-pole interference model, which also models the RFI as sinusoidal
tones. However the sinusoidal model only needs to be valid across the relatively
short filter length. Furthermore the filter only depends on spectral energy,
so the tap weights are not affected by the phase of the interference tone.
A further advantage is that the adaptive filter ``learns'' the environment.
It is claimed that the interference suppression filter can be superior
to the tone extractor [1]. A disadvantage of using
a filter approach is the reduction in record length because of edge effects.
Le et al [10] have implemented an LMS adaptive
filter with very good results. The filter performance with respect to the
filter parameters is analysed in terms of the radar performance parameters
such as the integrated sidelobe ratio (ISLR) and peak sidelobe
ratio (PSLR).
4 The LMS Adaptive Filter
Adaptive filters have been widely used in interference suppression applications
[1, 6, 10,
11, 16]. In contrast to fixed
filters, they have the desired ability to adjust their own parameters automatically.
Little or no a priori knowledge of the signal or noise characteristics
is required. It is, however, assumed that the interference is sinusoidal.
The adaptive filter relies on a recursive algorithm, which, in a stationary
environment, converges to the optimum Wiener solution. In a non-stationary
environment, the algorithm offers a tracking capability, whereby it can
track time variations in the statistics of the input data.
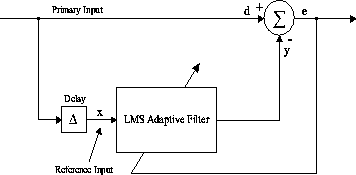 Figure 1: LMS Adaptive Filter
Figure 1: LMS Adaptive Filter
Figure 1 shows a schematic of the LMS adaptive
filter as it is used for RF interference cancelling. It requires a primary
input d and a reference input x, which is obtained by delaying
the primary input for some time delay  . The adaptive linear combiner weighs and sums a set of input signals to
form an adaptive output. The n-element input signal vector
. The adaptive linear combiner weighs and sums a set of input signals to
form an adaptive output. The n-element input signal vector  and the weight vector
and the weight vector 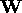 are defined at time j as follows:
are defined at time j as follows:
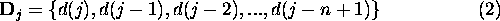
and
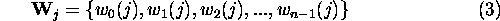
The reference signal vector 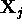 is defined as
is defined as

The output y(j) of the filter is equal to the inner product
of the row vectors 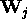 and
and 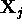
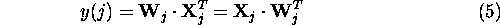
This output is an estimate of the RF interference. The error signal
e(j), which is the desired cleaned radar signal, is obtained
by subtracting the RF interference estimate from the primary input d(j)
according to
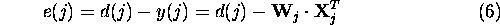
The LMS adaptive algorithm minimises the mean-square error e(j)
by recursively altering the weight vector 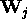 at each sampling instant according to the Widrow-Hoff algorithm [15],
yielding
at each sampling instant according to the Widrow-Hoff algorithm [15],
yielding
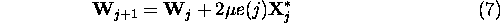
where the * symbol designates complex conjugation and 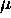 is a convergence factor controlling stability and rate of adaptation. A
larger value of
is a convergence factor controlling stability and rate of adaptation. A
larger value of 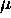 increases the rate of convergence, but also leads to a larger final misadjustment,
which is a quantitative measure of the amount by which the final value
of the mean-squared error deviates from the minimum mean-squared error
that is produced by the optimum Wiener filter.
increases the rate of convergence, but also leads to a larger final misadjustment,
which is a quantitative measure of the amount by which the final value
of the mean-squared error deviates from the minimum mean-squared error
that is produced by the optimum Wiener filter.
5 Simulation Setup and Results
The adaptive filter was applied on simulated data to verify its suitability
for RF interference suppression. Table 1 lists the
relevant radar parameters of the simulation. These parameters correspond
to the real P-Band data analysed in Section 6. The
optimum filter parameters can then be used for suppressing the RF interference
in the P-Band data.
Table 1: Radar Parameters of simulated
and P-Band Data
| centre frequency |
450 MHz |
| chirp bandwidth |
18 MHz |
| pulse length |
5 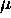 s
s |
| A/D (complex) sample rate |
60 MHz |
| range bins |
2048 |
The simulation was assembled as follows: A clean signal (see first
column of Figure 2) representing the ideal return
of a single point target was injected with basebanded RF ``interference''
in the form of five pure sinusoids at frequencies -8, -5, -1, 4 and 9MHz
with corresponding interference-to-signal amplitude ratios of 6, 2, 7,
4 and 5dB respectively and with random phase (see second column of Figure
2). White noise with a SNR of 20dB was also added.
This contaminated signal was fed to the adaptive filter (see third column
of Figure 2), and the performance of the filter
was evaluated by range compressing the filter output and measuring the
target mainlobe width, the peak sidelobe ratio (PSLR) and the integrated
sidelobe ratio (ISLR), measured across 200 range bins.
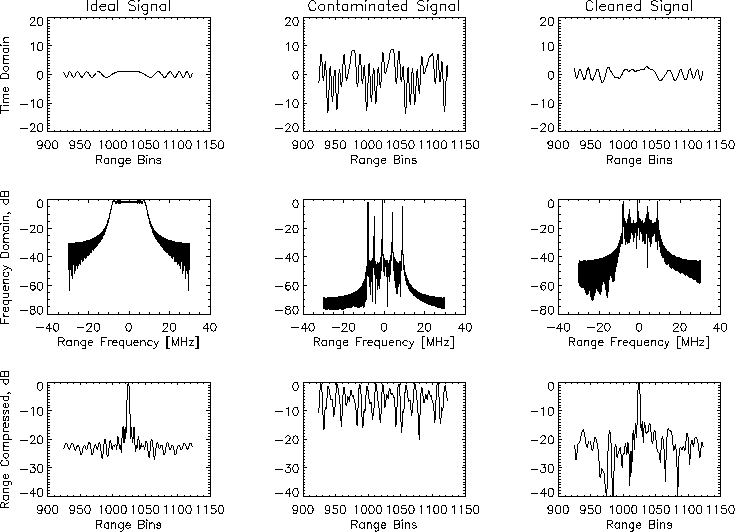 Figure 2: Simulation results demonstrating the effectiveness
of the adaptive filter applied to RF
interference suppression. The three columns show the ideal, contaminated
and cleaned signal
respectively. The first row shows the real part of the signal in
the time domain, the second row
shows the signal in the frequency domain, and the third row shows
the range compressed signal.
Figure 2: Simulation results demonstrating the effectiveness
of the adaptive filter applied to RF
interference suppression. The three columns show the ideal, contaminated
and cleaned signal
respectively. The first row shows the real part of the signal in
the time domain, the second row
shows the signal in the frequency domain, and the third row shows
the range compressed signal.
5.1 Filter Performance
Table 2 gives an indication of how the radar performance
is affected by the number of filter weights and the convergence factor  . The delay
. The delay  has not been included, since it was found that a delay of one time sample
was sufficient, and larger values of
has not been included, since it was found that a delay of one time sample
was sufficient, and larger values of 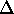 did not affect the results significantly. It has to be noted that the value
of
did not affect the results significantly. It has to be noted that the value
of 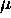 is inversely dependent on the amplitude of the input vector, and therefore
the absolute value is not as important as the relative change with respect
to the number of weights. Furthermore, as the number of weights increases,
the value of
is inversely dependent on the amplitude of the input vector, and therefore
the absolute value is not as important as the relative change with respect
to the number of weights. Furthermore, as the number of weights increases,
the value of 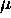 needs to be decreased appropriately, otherwise the filter output becomes
unstable. This can be seen in Table 2 with 256 weights
and
needs to be decreased appropriately, otherwise the filter output becomes
unstable. This can be seen in Table 2 with 256 weights
and 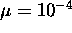 . Generally the performance increases as
. Generally the performance increases as 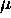 decreases. However if
decreases. However if 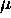 becomes too small, the weights do not converge, which also yields poor
performance. This was the case with 20 weights and
becomes too small, the weights do not converge, which also yields poor
performance. This was the case with 20 weights and 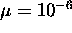 . The results also improve as more weights are used, however this increases
computation time and edge effects.
. The results also improve as more weights are used, however this increases
computation time and edge effects.
Table 2: Radar Performance vs Filter
Parameters
| Filter Parameters |
Radar Performance |
| weights |
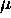 |
ML Width |
PSLR |
ISLR |
| |
|
[range bins] |
[dB] |
[dB] |
| 20 |
1e-4 |
3.1 |
-5.30 |
3.09 |
| 20 |
1e-5 |
3.2 |
-7.27 |
1.20 |
| 20 |
1e-6 |
3.4 |
-1.73 |
10.2 |
| 100 |
1e-4 |
2.9 |
-3.08 |
7.15 |
| 100 |
1e-5 |
3.1 |
-9.97 |
-0.68 |
| 100 |
1e-6 |
3.2 |
-12.4 |
-0.63 |
| 256 |
1e-4 |
unstable |
unstable |
unstable |
| 256 |
1e-5 |
3.0 |
-7.89 |
0.40 |
| 256 |
1e-6 |
3.2 |
-12.9 |
-2.78 |
Figure 2 graphically illustrates the results
that were obtained with 256 weights and 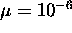 . The first column displays the ideal signal, without any interference.
The second column displays the contaminated signal, with the spectrum completely
dominated by noise and interference. The point target is not detectable
in the range compressed signal shown in the last row. The third column
shows the output of the adaptive filter, which is clearly a vast improvement
compared to the noisy signal. Looking at the second row, the filter has
significantly suppressed the spikes caused by the sinusoidal interferences.
The point target is clearly visible in the range compressed signal, with
the peak sidelobe being -12.9dB below the mainlobe, using a rectangular
weighting window.
. The first column displays the ideal signal, without any interference.
The second column displays the contaminated signal, with the spectrum completely
dominated by noise and interference. The point target is not detectable
in the range compressed signal shown in the last row. The third column
shows the output of the adaptive filter, which is clearly a vast improvement
compared to the noisy signal. Looking at the second row, the filter has
significantly suppressed the spikes caused by the sinusoidal interferences.
The point target is clearly visible in the range compressed signal, with
the peak sidelobe being -12.9dB below the mainlobe, using a rectangular
weighting window.
5.2 Performance Optimisation
The adaptive filter has been modified as follows in order to improve the
performance measured in terms of the PSLR and ISLR:
-
The range compressed output of the adaptive filter sometimes displayed
one very prominent sidelobe. In order to minimise this effect, the adaptive
filter was swept through the input vector from both ends, using two separate
weight vectors, after which the two output vectors were averaged. This
yielded significant performance improvements in terms of peak sidelobe
reduction.
-
Smaller values of
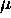 generally yielded better results, in terms of lower PSLR and ISLR. Sometimes,
however, this resulted in the tap weights not converging after one sweep
through the input vector, consisting of 2048 range bins. Therefore the
adaptive filter was applied to the data twice, using the weight values
of the first sweep as starting values for the second sweep.
generally yielded better results, in terms of lower PSLR and ISLR. Sometimes,
however, this resulted in the tap weights not converging after one sweep
through the input vector, consisting of 2048 range bins. Therefore the
adaptive filter was applied to the data twice, using the weight values
of the first sweep as starting values for the second sweep.
-
In order to minimise the edge effects of the filter, the input vector
was zero padded by the appropriate amount.
These filter modifications had an adverse effect in terms of computational
efficiency. Future research will entail the investigation of methods to
improve computational speed, such as using the same weight vector over
many range lines (presuming the interference is relatively constant), and
adaptively modifying the convergence factor 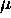 by monitoring how fast the weight vector changes.
by monitoring how fast the weight vector changes.
6 P-Band Data Analysis
Figure 5 shows a P-Band image in the vicinity of
Weilheim, Germany, which is severely degraded by RF interference. The image
was generated by the experimental airborne SAR system E-SAR of the DLR,
and the raw data was supplied to the authors by the DLR, Oberpfaffenhofen,
Germany. The RF interference in the image is clearly visible as bright
lines in the range direction. The interference is more dominant at the
far range due to sensitivity time control (STC). To obtain an estimate
of the number of interfering sources, 100 range spectra were averaged.
Since the interference remains relatively constant across a number of range
lines, averaging a number of spectra enhances the visibility of the interference.
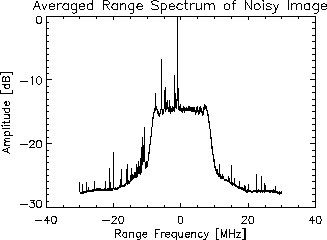 Figure 3: Averaged Range Spectrum of Noisy Image
Figure 3: Averaged Range Spectrum of Noisy Image
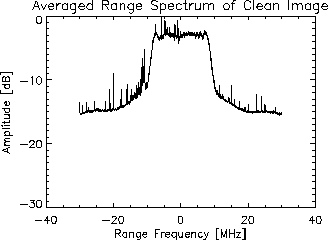 Figure 4: Averaged Range Spectrum of Cleaned Image
Figure 4: Averaged Range Spectrum of Cleaned Image
From Figure 3 one can see that there is
a large interference spike near the origin, and about 15 smaller spikes
on either side of the origin. After the image had been cleaned with a 512-tap
adaptive filter, the same 100 range spectra were averaged, yielding the
result shown in Figure 4. The large interference
spike has been reduced by about 12dB, which is a significant improvement.
However smaller interference spikes are still visible.
Figure 6 displays the cleaned P-Band image,
which is definitely a vast improvement. Some features that were hidden
by the interference have become visible, although sidelobes of bright targets
have also become more pronounced. Future work will concentrate on reducing
these sidelobes.
 Figure 5: P-Band image in the vicinity of Weilheim, Germany,
degraded by RF interference.
The flight path is along the horizontal axis, with near range towards
the bottom of the image.
The raw data was supplied by the DLR, Oberpfaffenhofen, Germany.
Figure 5: P-Band image in the vicinity of Weilheim, Germany,
degraded by RF interference.
The flight path is along the horizontal axis, with near range towards
the bottom of the image.
The raw data was supplied by the DLR, Oberpfaffenhofen, Germany.
 Figure 6: The same image after applying the LMS adaptive
filter to cancel the interference.
Figure 6: The same image after applying the LMS adaptive
filter to cancel the interference.
7 Conclusions
This paper has looked at a number of techniques that have been implemented
to suppress RF interference, but only the LMS adaptive filter has been
implemented and studied in detail, partly because of its ease of implementation,
and partly because of its favourable review in the literature.
It has been found that the adaptive filter does significantly suppress
RF interference, although sidelobes are enhanced. Future work will entail
looking at further enhancements to the algorithm, like sidelobe reduction
and computational efficiency.
Acknowledgments
Special thanks go to Stefan Buckreuss from the DLR for supplying the raw
P-Band E-SAR data, and for his help with processing the data. The authors
would also like to thank Jasper Horrell for his extensive help with processing
the data, as well as Andrew Wilkinson for his stimulating discussions on
the subject.
References
-
1
-
K. Abend and J. McCorkle, ``Radio and TV interference extraction for ultra-wideband
radar,'' in Algorithms for Synthetic Aperture Radar Imagery II (D.A.
Giglio, ed.), SPIE, Orlando, FL, vol. 2487, pp. 119-129, April 1995.
-
2
-
M. Braunstein, J. Ralston and D. Sparrow, ``Signal processing approaches
to radio frequency interference (RFI) suppression,'' in Algorithms for
Synthetic Aperture Radar Imagery (D.A. Giglio, ed.), SPIE, Orlando,
FL, vol. 2230, pp. 190-208, April 1994.
-
3
-
S. Buckreuss, ``Filtering Interferences from P-Band SAR Data,'' Proc.
European Conference on Synthetic Aperture Radar, EUSAR'98, Friedrichshafen,
Germany, pp. 279-282, May 1998.
-
4
-
G. Cazzaniga and A.M. Guarnieri, ``Removing RF interferences from P-Band
airplane SAR data,'' Proc. IEEE Geoscience Remote Sensing Symp., IGARSS'96,
Lincoln, Nebraska, vol. 3, pp. 1845-1847, June 1996.
-
5
-
B.H. Ferrell, ``Interference Suppression in UHF Synthetic-Aperture Radar,''
in Algorithms for Synthetic Aperture Radar Imagery II (D.A. Giglio,
ed.), SPIE, Orlando, FL, vol. 2487, pp. 96-106, April 1995.
-
6
-
J.R. Glover, Jr., ``Adaptive Noise Cancelling Applied to Sinusoidal Interferences,''
IEEE Transactions on Acoustics, Speech, and Signal Processing, vol.
ASSP-25, no. 6, pp. 484-491, December 1977.
-
7
-
A. Golden, Jr., S.A. Werness, M. Stuff, S. DeGraaf and R. Sullivan, ``Radio
frequency interference removal in a VHF/UHF deramp SAR,'' in Algorithms
for Synthetic Aperture Radar Imagery II (D.A. Giglio, ed.), SPIE, Orlando,
FL, vol. 2487, pp. 84-95, April 1995.
-
8
-
S. Haykin, Adaptive Filter Theory, 2nd edition, Prentice-Hall, Englewood
Cliffs, NJ, 1991.
-
9
-
T. Koutsoudis and L. Lovas, ``RF Interference Suppression in Ultra Wideband
Radar Receivers,'' in Algorithms for Synthetic Aperture Radar Imagery
II (D.A. Giglio, ed.), SPIE, Orlando, FL, vol. 2487, pp. 107-118, April
1995.
-
10
-
C.T.C. Le, S. Hensley and E. Chapin, ``Adaptive Filtering of RFI in Wideband
SAR Signals,'' 7th Annual JPL AirSAR Workshop, Pasadena, California,
January 1997.
-
11
-
J. Li and P. Stoica, ``Adaptive Filtering Approach to Spectral Estimation
and SAR Imaging,'' in Algorithms for Synthetic Aperture Radar Imagery
II (D.A. Giglio, ed.), SPIE, Orlando, FL, vol. 2487, pp. 153-164, April
1995.
-
12
-
S.L. Marple, Jr., Digital Spectral Analysis, Prentice-Hall, Englewood
Cliffs, NJ, 1987.
-
13
-
T. Miller, J. McCorkle and L. Potter, ``Near-least-squares radio frequency
interference suppression,'' in Algorithms for Synthetic Aperture Radar
Imagery II (D.A. Giglio, ed.), SPIE, Orlando, FL, vol. 2487, pp. 72-83,
April 1995.
-
14
-
J.M. Ralston, J.F. Heagy and R.J. Sullivan, ``Environmental Noise Effects
on VHF/UHF UWB SAR,'' Proc. European Conference on Synthetic Aperture
Radar, EUSAR'98, Friedrichshafen, Germany, pp. 141-144, May 1998.
-
15
-
B. Widrow and J. McCool, ``The Complex LMS Algorithm,'' Proc. Letters
of the IEEE, pp. 719-720, April 1975.
-
16
-
B. Widrow, J.R. Glover, Jr., J.M. McCool, J. Kaunitz, C.S. Williams, R.H.
Hearn, J.R. Zeidler, E. Dong, Jr., and R.C. Goodlin, ``Adaptive Noise Cancelling:
Principles and Applications,'' Proc. IEEE, vol. 63, no. 12, pp.
1692-1716, December 1975.
-
17
-
B. Widrow and S.D. Stearns, Adaptive Signal Processing, Prentice-Hall,
Englewood Cliffs, NJ, 1985.
-
-
-
-
Return to Richard Lord's Homepage.
-
-
-

![]() s, which is consistent with an effective bandwidth of a few hundred kHz
or less.
s, which is consistent with an effective bandwidth of a few hundred kHz
or less.
![]() can be found analytically, however for multiple sinusoids it becomes an
extremely difficult nonlinear problem involving 3m variables, where
m is the number of sinusoids to be estimated. An efficient technique
to overcome this problem is to use an iterative algorithm, where the initial
guess of the estimates is iteratively improved. The initial guess may be
obtained from the data spectrum by applying an FFT. Another method would
be to model the RFI, signal and noise as an autoregressive (AR)
process [1, 12]. The estimate
can be found analytically, however for multiple sinusoids it becomes an
extremely difficult nonlinear problem involving 3m variables, where
m is the number of sinusoids to be estimated. An efficient technique
to overcome this problem is to use an iterative algorithm, where the initial
guess of the estimates is iteratively improved. The initial guess may be
obtained from the data spectrum by applying an FFT. Another method would
be to model the RFI, signal and noise as an autoregressive (AR)
process [1, 12]. The estimate ![]() of the nth sample of the measured data is given by
of the nth sample of the measured data is given by
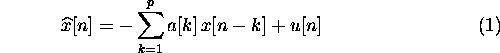

![]() . The adaptive linear combiner weighs and sums a set of input signals to
form an adaptive output. The n-element input signal vector
. The adaptive linear combiner weighs and sums a set of input signals to
form an adaptive output. The n-element input signal vector ![]() and the weight vector
and the weight vector ![]() are defined at time j as follows:
are defined at time j as follows:
![]()
![]()
![]() is defined as
is defined as
![]()
![]() and
and ![]()
![]()
![]()
![]() at each sampling instant according to the Widrow-Hoff algorithm [15],
yielding
at each sampling instant according to the Widrow-Hoff algorithm [15],
yielding
![]()
![]() is a convergence factor controlling stability and rate of adaptation. A
larger value of
is a convergence factor controlling stability and rate of adaptation. A
larger value of ![]() increases the rate of convergence, but also leads to a larger final misadjustment,
which is a quantitative measure of the amount by which the final value
of the mean-squared error deviates from the minimum mean-squared error
that is produced by the optimum Wiener filter.
increases the rate of convergence, but also leads to a larger final misadjustment,
which is a quantitative measure of the amount by which the final value
of the mean-squared error deviates from the minimum mean-squared error
that is produced by the optimum Wiener filter.




