Synthetic Range Profiling using the IFFT Approach

Richard T. Lord and Michael R. Inggs
Radar Remote Sensing Group, Dept of Electrical Engineering, University of Cape Town
Private Bag, Rondebosch 7701, South Africa
Tel: +27 21 650 2799   Fax: +27 21 650 3465
Email:  rlord-avoidspam@ebe.uct.ac.za
 
 
 
Note --- This paper has been published at the Igarss'96 conference.  A pdf version of this paper can be downloaded here: igarss96.pdf
 
 
Abstract --- This paper demonstrates the use of stepped-frequency waveforms to obtain high resolution SAR images without imposing severe instantaneous bandwidth requirements on the radar system.  Although azimuth compression and motion compensation are essential to obtain high resolution SAR images, this paper only discusses how to obtain high range resolutions.  Especially at VHF frequencies it is very difficult to obtain high range resolutions, because the effective pulse bandwidth required would amount to a large percentage of the centre frequency.  After briefly introducing the theory of synthetic range profiling as applied to SAR, this paper goes on to discuss the synthetic range profile of an A320 airbus, which serves to demonstrate the feasibility of synthetic range profiling.  More attention is then given to simulation results, which introduce the problems encountered when sampling the returning echo waveforms.
 

I. Introduction

 
Synthetic range profiling (SRP) is a processing technique to obtain high range resolution using stepped-frequency waveforms without imposing severe instantaneous bandwidth requirements on the radar system.  A total radar bandwidth of 64 x 1.5 = 96 MHz can be synthesized by sequentially transmitting 64 pulses, each pulse stepped in frequency by 1.5 MHz.  The final slant-range resolution that can therefore be achieved is about 1.56m.
 
 
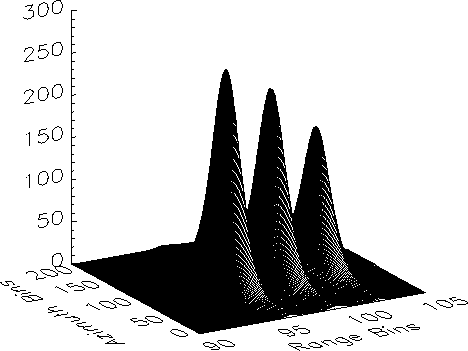 figure5
 
Figure 1: Surface plot of three point targets that were resolved using synthetic range profiling.
 
 
This is illustrated in Fig. 1, which shows a surface plot of three point targets that were resolved using SRP.  These simulated point targets, which were 6m apart in ground range, were "illuminated'' with 64 monochrome pulses stepped in frequency, each pulse having a bandwidth of 1.5 MHz, which corresponds to a slant-range resolution of only 100m.  However the use of stepped-frequency processing yielded a final slant-range resolution of 1.56m.

The CARABAS system is a practical example of an airborne SAR system which operates in the lower part of the VHF-band to produce surface images using stepped-frequency waveforms [2].
 

II. Synthetic Range Profiling Applied to SAR

 
To produce SAR images with stepped-frequency waveforms basically requires the production of one SRP per coarse range bin.  Obtaining a SRP involves the following steps [5]:
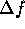  1. Transmit a burst of n pulses, each pulse shifted in frequency by a fixed frequency step size tex2html_wrap_inline129 .
  2. Collect one I and Q sample of the target's baseband echo response in each coarse range bin for every transmitted pulse.  These samples are the frequency-domain measurements of the target's spectral profile.
  3. Apply an inverse discrete Fourier transform (IFFT) on the n complex samples in each coarse range bin to obtain an n-element SRP of the target in the respective coarse range bin.
In contrast with data obtained from pulse-compression radars, the data is already compressed in the range direction at this stage, since the slant-range resolution has been obtained synthetically using the inverse discrete Fourier transform.  The azimuth resolution, however, can be obtained as in pulse-compression radars by coherently integrating the range-resolved echo signals that were obtained during the real beam dwell time.  This aspect is not addressed in this paper.  Furthermore, to obtain high resolution images, motion compensation and range curvature would have to be addressed as well.  Another problem not discussed in this paper is the variation of the radar response with frequency and observation angle [1], which varies significantly over the synthetic aperture path.

The synthetic slant-range resolution is given by

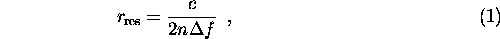
equation16

and the slant-range ambiguity length is given by

equation21

Ideally the matched filter integration length, given by 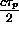tex2html_wrap_inline141 , where 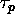tex2html_wrap_inline143 is the pulse length, should equal the slant-range ambiguity length 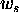tex2html_wrap_inline145 .  This leads to a pulse length of

equation27

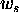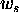When the integration length is greater than tex2html_wrap_inline145 , foldover will occur due to integration of scatterers outside the unambiguous range length.  However if the integration length is smaller than tex2html_wrap_inline145 , the echo signal will only contain energy integrated from a range depth smaller than the slant-range ambiguity length.
 

III. Synthetic Range Profiles of Aeroplanes

 
The feasibility of using stepped-frequency waveforms to produce high resolution down-range profiles has already been demonstrated by the production of SRPs of aeroplanes [4].  Fig. 2 shows the SRP of an A320 airbus that has been produced by transmitting linear chirp pulses at 55 different frequencies at L-Band.  Two pulses were transmitted at each frequency in order to carry out moving target indication (MTI) processing.  Each pulse had a bandwidth of 3.6364 MHz, which resulted in a compressed pulse width of 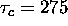tex2html_wrap_inline151 ns.  The pulse resolution was therefore 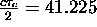tex2html_wrap_inline153 m, which is about the length of a large aircraft.
 
 
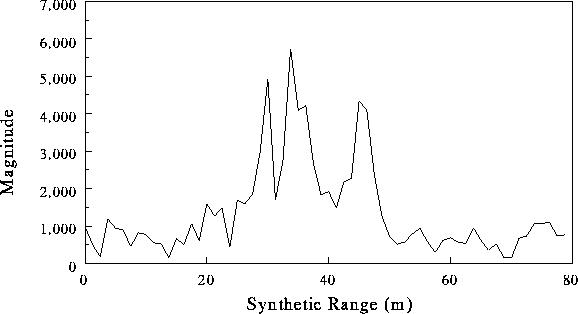 figure36
 
Figure 2: Synthetic Range Profile of an A320 airbus.
 
 
The frequency spacing was 1.875 MHz, which corresponds to a range-delay extent of 80m, which is about twice the length of the pulse resolution.  The total processed radar bandwidth was 103.125 MHz, which results in a slant-range resolution of 1.45m.
 

IV. Simulation Results

 
Table I gives the parameters that were used to obtain the simulated SAR data.
 
Table I: Parameters of radar using SRP
 
  Frequency Step Size  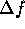 tex2html_wrap_inline129    1.5 MHz 
  Number of Steps    n    64 
  Start Frequency  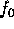 tex2html_wrap_inline161    90.75 MHz 
  Stop Frequency  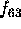 tex2html_wrap_inline163    185.25 MHz 
  Total Radar Bandwidth    B    96 MHz 
  Slant-Range Resolution  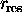 tex2html_wrap_inline167    1.56 m 
  A/D sampling frequency  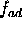 tex2html_wrap_inline169    1.5 MHz 
  Coarse Range Bin Size  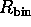 tex2html_wrap_inline171    100 m 
  Pulse Length  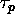 tex2html_wrap_inline143    666.67 ns 
  Pulse Repitition Frequency    PRF    11.52 kHz 
 
 
Fig. 3 shows the magnitude along a range line of a single resolved point target.
 
 
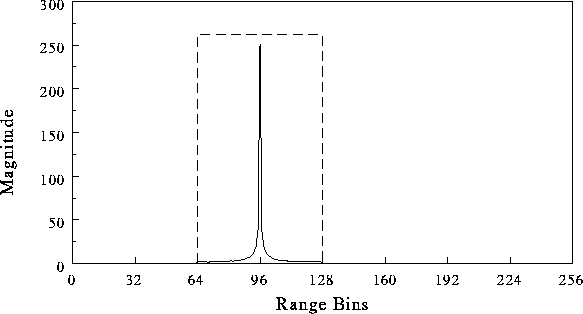 figure55
 
Figure 3: Synthetic range profile of a single point target in one coarse range bin.
 
 
The dashed line indicates the coarse range bin in which the point target is situated.  Samples were collected in four successive coarse range bins, each bin having a slant-range extent of 100m (corresponding to a 667ns pulse).  Note that the instantaneous bandwidth and the A/D sampling frequency required are only 1.5 MHz, compared with the final processed bandwidth of 96 MHz.  The original PRF of 180Hz was increased by a factor of 64, giving a final PRF of 11.52kHz.  A radar mounted on an aircraft which flies at a height of 10km, mapping out a 4km wide swath in slant range, requires a PRF of less than 37.5kHz to avoid ambiguity problems.  However if it is required that one pulse has to be received before the next pulse is transmitted, this increase in PRF will be unacceptable.  The technique of multiple PRF ranging [3 pg. 116] may be used to solve this problem.

In Fig. 4 a range line displaying three resolved targets is shown.  The important thing to note in Fig. 4 is the spill-over of energy into the successive range bin.  The next section discusses this problem in more detail.
 
 

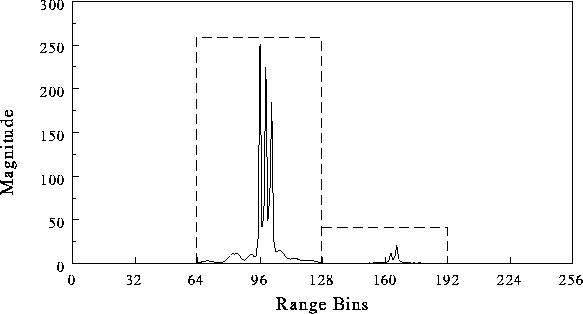 figure62
 
Figure 4: Synthetic range profile of three point targets in one coarse range bin,
showing spill-over of energy into successive range bin.
 
 

V. Sampling Criteria

 
Fig. 5 shows that for a single point target it is possible to avoid spill-over of energy into the successive range bin by sampling the matched filter output exactly at the peak of the triangular waveform.  This scenario was followed when the data of Fig. 3 was produced.  However as soon as there is more than one point target (which is the case in practice), there will be an inevitable spill-over of energy into the next range bin, as illustrated in Fig. 5.  Sampling still takes place at the theoretical peak of the first pulse, but some of the energy of the second pulse and even more energy of the third pulse is also sampled in the next coarse range bin.  This explains the decrease in amplitude of the second and third pulse as seen in Fig. 4.
 
 
 
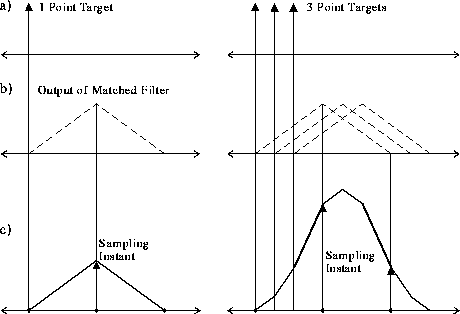 figure69
 
 Figure 5: Sampling the output of the matched filter.
 

A solution to the problem of spill-over of energy would be to sample every second coarse range bin during one transmitted pulse, and then every other second coarse range bin during the next transmitted pulse.  This, however, will increase the PRF by a factor of two.  Further investigations are being carried out using windowing functions and overlapping coarse range bins, in order to arrive at a satisfactory solution regarding the sampling of returning waveforms.
 

VI. Skipping Frequencies

 
An important advantage of using stepped-frequency waveforms is the capability of skipping certain frequencies that would otherwise be corrupted by external sources such as broadcast FM and mobile radio.  Before transmitting a pulse, the receiver could predict how much interference there will be at a particular frequency, and then decide to skip that frequency.  Since the order in which frequencies are transmitted is not important, the radar could try to transmit a skipped frequency at a later stage in the burst.  Another way out would be to interpolate the I and Q values of skipped pulses from those I and Q values of surrounding pulses.
 

VII. Conclusions

 
The results that have been obtained from simulated SAR data show that it is feasible to use stepped-frequency waveforms to produce high resolution VHF SAR images.  Not only do stepped-frequency waveforms alleviate the instantaneous bandwidth requirements of the radar system, but they also offer the capability of skipping frequency regions that might be polluted by external sources.  This is expected to be a major feature of such a system, since the amount of interference at the VHF band is expected to be quite severe.

Further work will have to be carried out to investigate the effects of interpolating missing pulses, to solve the problems of the matched filter effect satisfactorily, to investigate the use of multiple PRF ranging and to implement high resolution SAR azimuth processing.
 

References

 
  1. S.R.J. Axelsson, "Frequency and Azimuthal Variations of Radar Cross Section and Their Influence Upon Low-Frequency SAR Imaging,'' IEEE Trans. on Geoscience and Remote Sensing, vol. 33, no. 5, pp. 1258-1265, September 1995.
  2. A. Gustavsson, P.O. Frölind, H. Hellsten, T. Jonsson, B. Larsson and G. Stenström, "The Airborne VHF SAR System CARABAS,'' Proc. IEEE Geoscience Remote Sensing Symp., IGARSS'93, Tokyo, Japan, vol. 2, pp. 558-562, August 1993.
  3. S.A. Hovanessian, Radar System Design and Analysis, Norwood, MA 02062: Artech House, 1984.
  4. A.D. Robinson and M.R. Inggs, "Correlation Filters Applied to Synthetic Range Profiles of Aircraft Targets,'' Proc. of the IEEE South African Communications and Signal Processing Symp., COMSIG'94, October 1994.
  5. D.R. Wehner, High Resolution Radar, Norwood, MA 02062: Artech House, 1987.
 
 
Return to Richard Lord's Homepage.